Operations on Random Variables
Apart from just creating wrapper code around sampling procedures which represent random variables, it is also important to do transformations on random variables to yield new more interesting random variables and distributions. In statistics one often formulates certain random variables as algebraic operations on other simpler random variables.
Algebraic Operations¶
It is possible to do common algebraic operations on instances of continuous random variables.
import spire.implicits._
val b = RandomVariable(new Beta(7.5, 7.5))
val g = RandomVariable(new Gamma(1.5, 1.2))
val n = GaussianRV(0.0, 1.0)
val addR = b + n - g
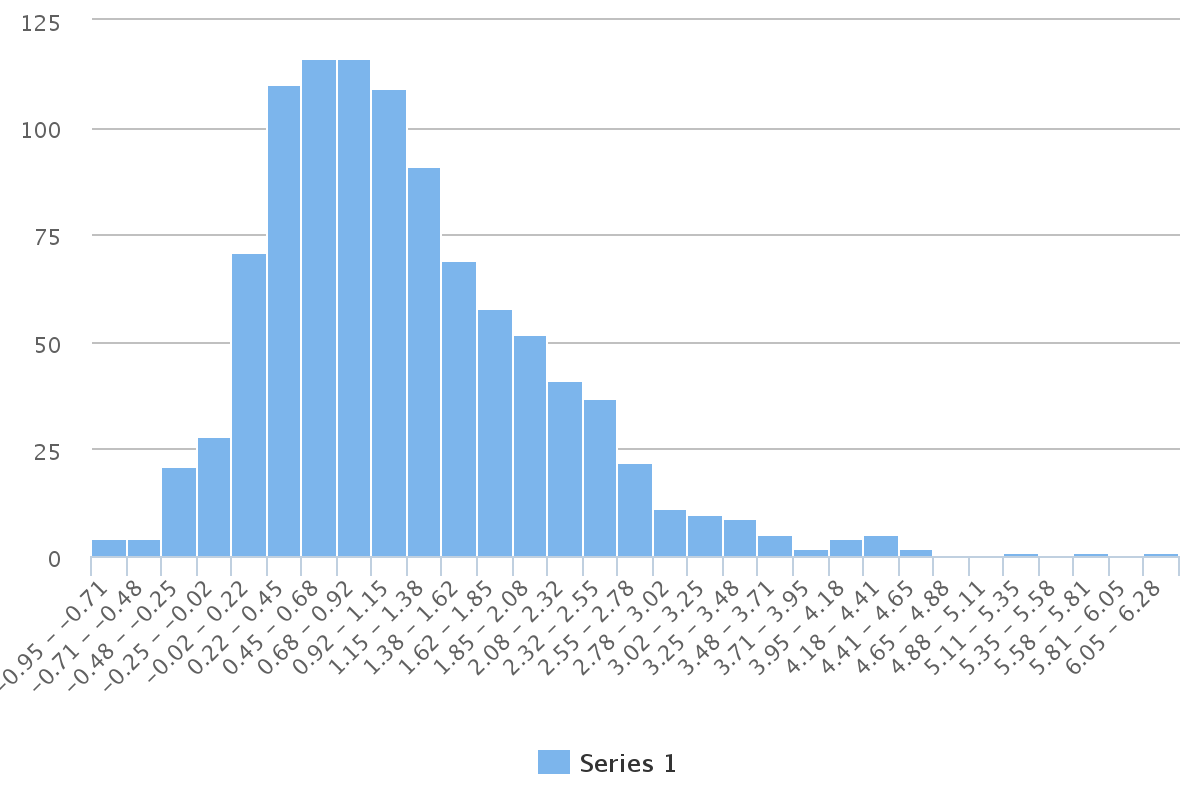
val multR = b * (n + g)
histogram((1 to 1000).map(_ => multR.sample()))
Measurable Functions¶
In many cases random variables can be expressed as functions of one another, for example chi square random variables are obtained by squaring normally distributed samples.
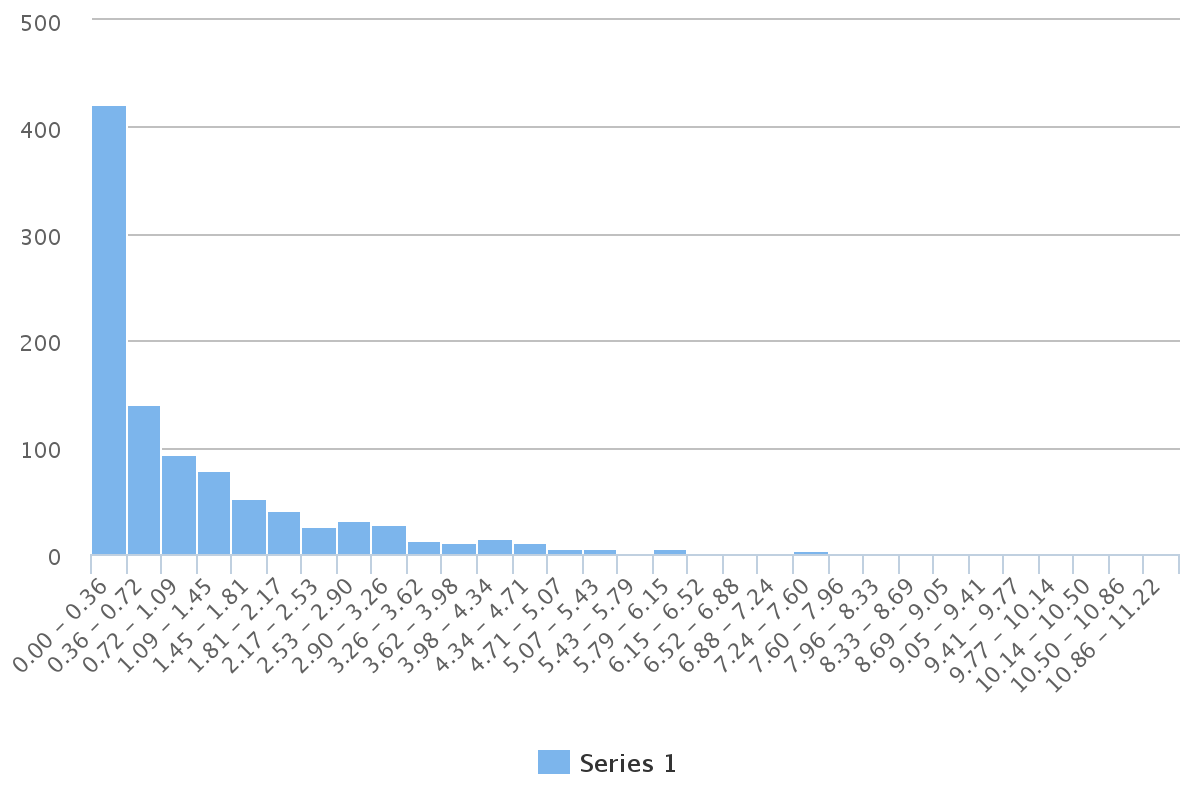
val chsq = MeasurableFunction(n, DataPipe((x: Double) => x*x))
//Generate a chi square distribution with one degree of freedom
histogram((1 to 1000).map(_ => chsq.sample()))
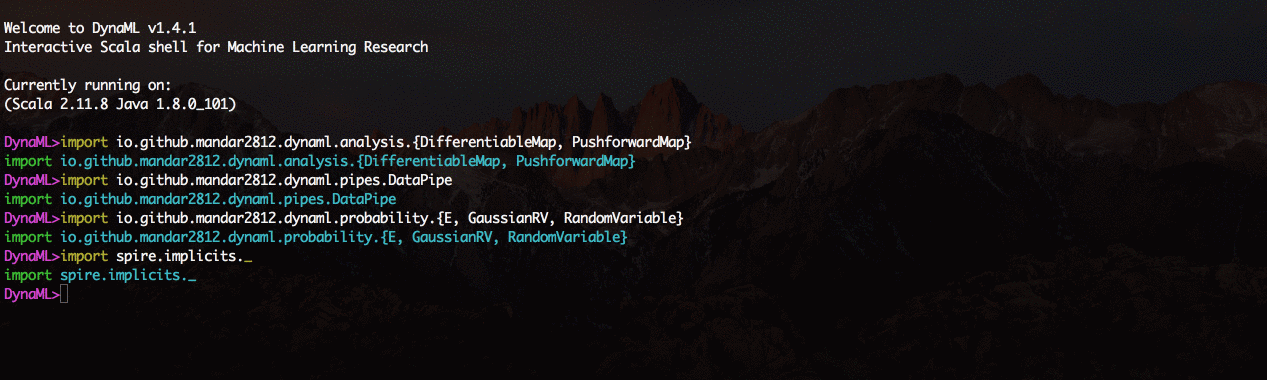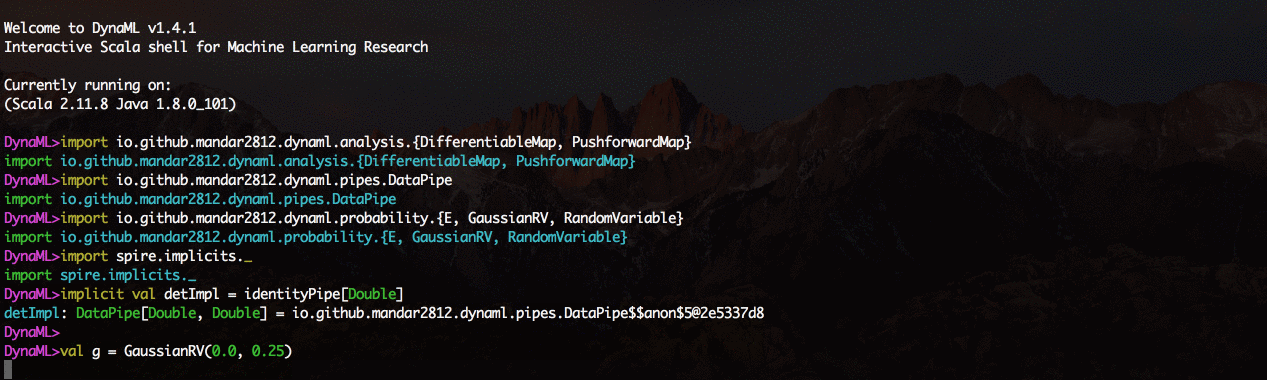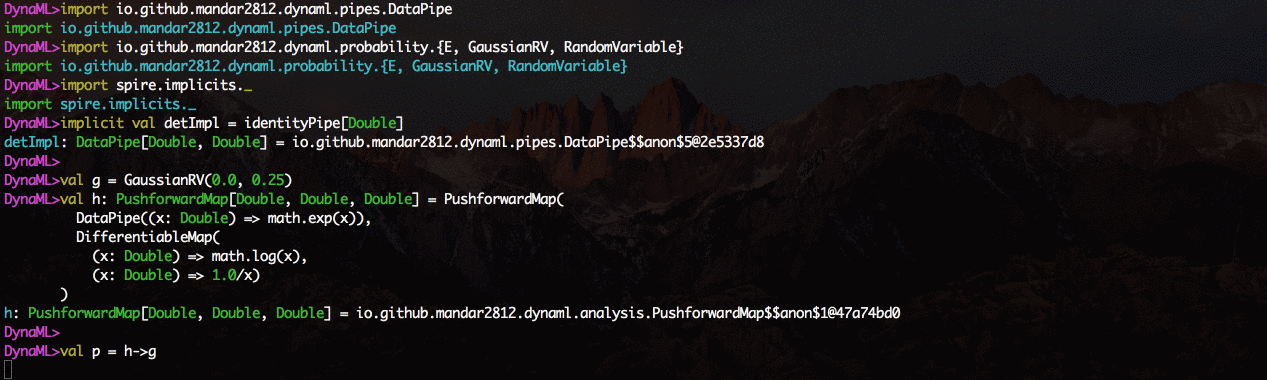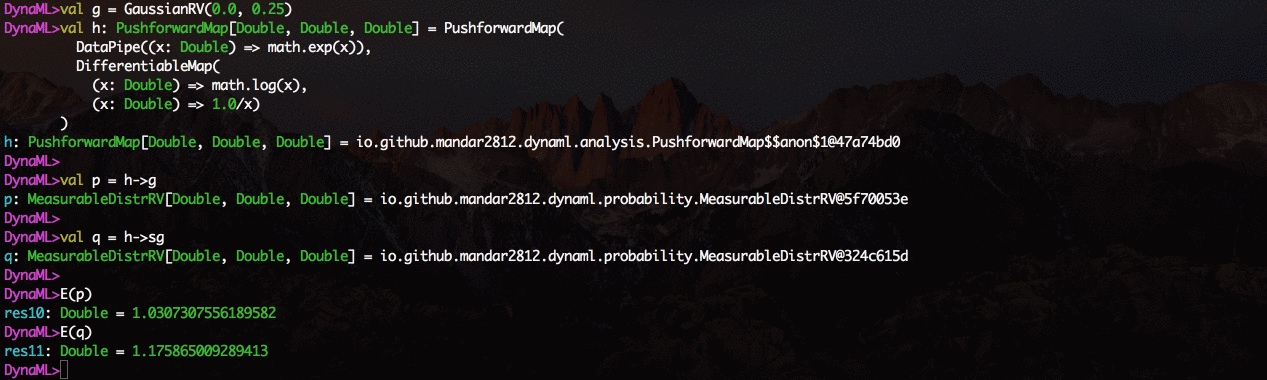
Push-forward Maps¶